Queues, Deques and Priority Queues:

Queue is a linear list of elements in which the deletion can take place only at one end, called the FRONT and the insertion can takes place only at the other end called the REAR.  The term FRONT and REAR are used in describing a linear list only when it is implemented as a queue.

Queues are also called as First in First out (FIFO) list, since the first element in a queue will be the first element out of the queue.  Another word, the order in which elements entered a queue is the order in which they leave.

Queues abound in everyday life. The automobile waiting to pass through an interaction for a queue, in which the first car in line is the first car through. The people waiting in the line at a bank from a queue, where the first person in line is the first person to be waited on and so on.

An important example of queue in computer science occurs in a time sharing system, in which the program with the same priority from a queue while waiting to be executed.

Fig. Queues

Representation of queues:

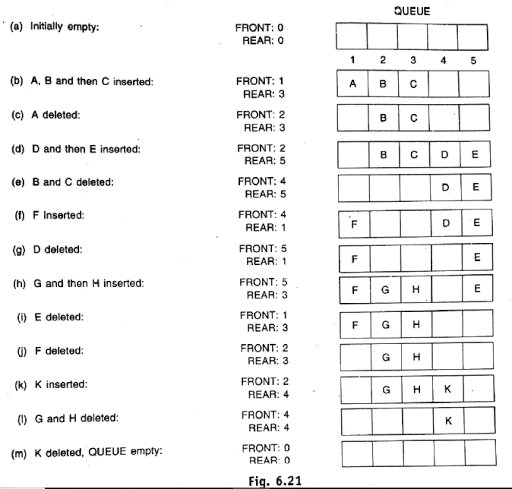
Queue may be represented in a computer in various ways usually by means of one way list or linear array.  Each of our queues will be maintained by a linear array QUEUE and to pointer variable: FRONT, contain the location of the front element of the queue, and REAR, containing the location of the rear element of the queue. 

The condition FRONT=NULL will indicate that the queue is empty.

The element will be deleted from the queue and the way new element will be added to the queue .Observe that whenever an element is deleted from the queue, the value of FRONT is incremented by 1.  This can be implemented by the assignment.

 

FRONT: =FRONT+1

Similarly, whenever an element is added to the queue,  the value of rear is incremented by 1.

REAR: =REAR+1

This means that after n insertion, the rear element of the queue will occupy QUEUE [N], or, another word;  eventually the Q will occupy the last part of the array.

Suppose we want to insert an element ITEM into a queue at the time the queue does occupy in last part of the array, i.e when REAR=N.  One way to do this is to simply move the entire Q to the beginning of the array, by changing front and rear accordingly, and then inserting item as above. This procedure may be very expensive the procedure we adopt is to assume that the Q is circular. That is Q[1] comes after Q[N] in the array. With this assumption, we insert item into the queue by assigning ITEM to QUEUE [1].  Specifically, instead of increasing REAR to N+1, we reset REAR=1 and then assign

                QUEUE[REAR]:=ITEM

Similarly, if front= N and an element of queue is deleted, we reset FRONT=1 instead of increasing FRONT to N+1.

Suppose that our queue contain only one element i.e 

            

                FRONT=REAR!=NULL

 And suppose that the element is deleted.  then we assign

FRONT=NULL and REAR= NULL  to indicate that the queue is empty.

Algorithm to insert an Item into a Queue:

QINSERT (QUEUE, N, FRONT, REAR, ITEM)

This procedure inserts an element ITEM into a queue.

1.  [Queue already filled?]

     If FRONT=1 and REAR=N, or FRONT=REAR+1, then:

            Write: OVERFLOW, and Return.

2. [Find new value of REAR]

       If FRONT: =NULL, then:[Queue initially empty]

            Set FRONT: =1 and REAR: =1

Else if REAR: =N, then:

            Set REAR: =1

Else

            Set REAR: = REAR+1.

[End of if structure]

3. Set QUEUE[REAR]:=ITEM [This inserts new element]

4.  Return.

Algorithm to delete an Item from a Queue:

QDELETE (QUEUE, N, FRONT, REAR, ITEM)

This procedure deletes an element ITEM from a queue.

1.  [Queue already empty?]

If FRONT=NULL, then:

            Write: UNDERFLOW, and Return.

2. Set ITEM := QUEUE[FRONT]

3.[Find new value of FRONT]

       If FRONT: =REAR, then:[Queue has only one element]

            Set FRONT: =NULL and REAR: =NULL

Else if FRONT: =N, then:

            Set FRONT: =1

Else

            Set FRONT: = FRONT+1.

[End of if structure]

4. Return

DEQUES:

A deque is a linear list in which the elements can be added or removed at either end but not in the middle.  The term deque is a contraction of the name double ended queue.

Deque  is maintained by a circular array DEQUE  with pointers left and right,  which points to the two ends of the deque.  We assume that the elements extend from the left end to the right end in the array.  The term circular comes from the fact that we assume that DEQUE[1]  comes after DEQUE[N]  in the array.  Picture shows the deque with N=8  memory location.  The condition LEFT=NULL will be used to indicate that deque is empty.

There are two variations of the deque- namely, an input restricted deque and output restricted deque - which are intermediate between deque and queue . Specifically, an input restricted deque is a deque, which allow insertion at only one end off the list but allow deletion at both the end of the list; and an output restricted deque is a deque which allows deletion at only one end of the list but allow insertion at both the ends of the list.

DEQUES

Priority Queues:

A priority queue is a collection of elements such that each element has been assign a priority and such that the order in which the element are deleted and processed comes from the following rules:

1. An element of higher priority is processed Before any element of lower priority
2. Two elements with the same priority are processed according to the order in which they were added to the queue.

A prototype of a priority queue is a time sharing system:  programs of higher priority or precede first and program with the same priority form standard queue. 

One way list representation of Priority Queue: 

One-way to maintain a priority queue in memory is by means of one way list,  as follows.

1. Each node in the list will contain three item of information:  and information field INFO, a Priority number PRN and link number LINK.
2. A node X proceeds in node Y in the list: 
1. When x has higher priority than y
2. When both have same priority but X was added to the list before y. This means that the order in the one-way list corresponds to the order of the priority queue

One-way List Representation of Priority Queue

Array representation of Priority Queue:

Another way to maintain a priority queue in memory is to use a separate queue for each level of priority.  Each such you will appear in its own circular array and must have its own pair of pointer, front and rear.  In fact, If each queue is allocated the same amount of space, if two dimensional array queue can be used instead of the linear array.

Figure shows this representation of priority queue.  Observe that FRONT [K] and REAR [K] contents, respectively, different and real elements of row K of QUEUE, the row that maintain the queue of elements with priority number k.

Array Representation of Priority Queue