Queues, Deques and Priority Queues:

Queue is a linear list of elements in which the deletion can take place only at one end, called the FRONT and the insertion can takes place only at the other end called the REAR.  The term FRONT and REAR are used in describing a linear list only when it is implemented as a queue.

Queues are also called as First in First out (FIFO) list, since the first element in a queue will be the first element out of the queue.  Another word, the order in which elements entered a queue is the order in which they leave.

Queues abound in everyday life. The automobile waiting to pass through an interaction for a queue, in which the first car in line is the first car through. The people waiting in the line at a bank from a queue, where the first person in line is the first person to be waited on and so on.

An important example of queue in computer science occurs in a time sharing system, in which the program with the same priority from a queue while waiting to be executed.

Fig. Queues

Representation of queues:

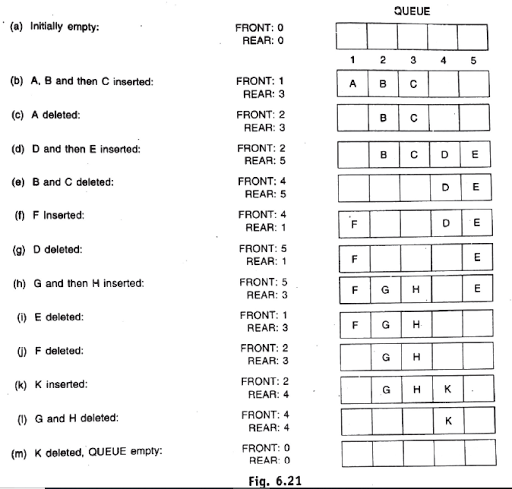
Queue may be represented in a computer in various ways usually by means of one way list or linear array.  Each of our queues will be maintained by a linear array QUEUE and to pointer variable: FRONT, contain the location of the front element of the queue, and REAR, containing the location of the rear element of the queue. 

The condition FRONT=NULL will indicate that the queue is empty.

The element will be deleted from the queue and the way new element will be added to the queue .Observe that whenever an element is deleted from the queue, the value of FRONT is incremented by 1.  This can be implemented by the assignment.

 

FRONT: =FRONT+1

Similarly, whenever an element is added to the queue,  the value of rear is incremented by 1.

REAR: =REAR+1

This means that after n insertion, the rear element of the queue will occupy QUEUE [N], or, another word;  eventually the Q will occupy the last part of the array.

Suppose we want to insert an element ITEM into a queue at the time the queue does occupy in last part of the array, i.e when REAR=N.  One way to do this is to simply move the entire Q to the beginning of the array, by changing front and rear accordingly, and then inserting item as above. This procedure may be very expensive the procedure we adopt is to assume that the Q is circular. That is Q[1] comes after Q[N] in the array. With this assumption, we insert item into the queue by assigning ITEM to QUEUE [1].  Specifically, instead of increasing REAR to N+1, we reset REAR=1 and then assign

                QUEUE[REAR]:=ITEM

Similarly, if front= N and an element of queue is deleted, we reset FRONT=1 instead of increasing FRONT to N+1.

Suppose that our queue contain only one element i.e 

            

                FRONT=REAR!=NULL

 And suppose that the element is deleted.  then we assign

FRONT=NULL and REAR= NULL  to indicate that the queue is empty.

Algorithm to insert an Item into a Queue:

QINSERT (QUEUE, N, FRONT, REAR, ITEM)

This procedure inserts an element ITEM into a queue.

1.  [Queue already filled?]

     If FRONT=1 and REAR=N, or FRONT=REAR+1, then:

            Write: OVERFLOW, and Return.

2. [Find new value of REAR]

       If FRONT: =NULL, then:[Queue initially empty]

            Set FRONT: =1 and REAR: =1

Else if REAR: =N, then:

            Set REAR: =1

Else

            Set REAR: = REAR+1.

[End of if structure]

3. Set QUEUE[REAR]:=ITEM [This inserts new element]

4.  Return.

Algorithm to delete an Item from a Queue:

QDELETE (QUEUE, N, FRONT, REAR, ITEM)

This procedure deletes an element ITEM from a queue.

1.  [Queue already empty?]

If FRONT=NULL, then:

            Write: UNDERFLOW, and Return.

2. Set ITEM := QUEUE[FRONT]

3.[Find new value of FRONT]

       If FRONT: =REAR, then:[Queue has only one element]

            Set FRONT: =NULL and REAR: =NULL

Else if FRONT: =N, then:

            Set FRONT: =1

Else

            Set FRONT: = FRONT+1.

[End of if structure]

4. Return

DEQUES:

A deque is a linear list in which the elements can be added or removed at either end but not in the middle.  The term deque is a contraction of the name double ended queue.

Deque  is maintained by a circular array DEQUE  with pointers left and right,  which points to the two ends of the deque.  We assume that the elements extend from the left end to the right end in the array.  The term circular comes from the fact that we assume that DEQUE[1]  comes after DEQUE[N]  in the array.  Picture shows the deque with N=8  memory location.  The condition LEFT=NULL will be used to indicate that deque is empty.

There are two variations of the deque- namely, an input restricted deque and output restricted deque - which are intermediate between deque and queue . Specifically, an input restricted deque is a deque, which allow insertion at only one end off the list but allow deletion at both the end of the list; and an output restricted deque is a deque which allows deletion at only one end of the list but allow insertion at both the ends of the list.

DEQUES

Priority Queues:

A priority queue is a collection of elements such that each element has been assign a priority and such that the order in which the element are deleted and processed comes from the following rules:

1. An element of higher priority is processed Before any element of lower priority
2. Two elements with the same priority are processed according to the order in which they were added to the queue.

A prototype of a priority queue is a time sharing system:  programs of higher priority or precede first and program with the same priority form standard queue. 

One way list representation of Priority Queue: 

One-way to maintain a priority queue in memory is by means of one way list,  as follows.

1. Each node in the list will contain three item of information:  and information field INFO, a Priority number PRN and link number LINK.
2. A node X proceeds in node Y in the list: 
1. When x has higher priority than y
2. When both have same priority but X was added to the list before y. This means that the order in the one-way list corresponds to the order of the priority queue

One-way List Representation of Priority Queue

Array representation of Priority Queue:

Another way to maintain a priority queue in memory is to use a separate queue for each level of priority.  Each such you will appear in its own circular array and must have its own pair of pointer, front and rear.  In fact, If each queue is allocated the same amount of space, if two dimensional array queue can be used instead of the linear array.

Figure shows this representation of priority queue.  Observe that FRONT [K] and REAR [K] contents, respectively, different and real elements of row K of QUEUE, the row that maintain the queue of elements with priority number k.

Array Representation of Priority Queue

Recursion

Recursion:

Suppose P is a procedure containing either call statement to itself or call statement to a second procedure that may eventually result in call statement back to the original procedure P then P is called as recursive procedure.

A recursive procedure must have the following two properties:

1. There must be a certain criteria, call base criteria, for which the procedure does not call to itself.
2. Each time the procedure does call itself, it must be closer to base criteria.

Similarly, a function is said to be a recursively define if function definition refers to itself.

 In order for the definition not to be circular, it has the following properties

1. There must be a certain augment, called base value.  For which function does not refers to itself.
2. Each time the function does refer to itself, the argument of the function must be closer to a base value.

Factorial function:

The product of the positive integer from 1 to n, is called ‘n factorial’ and usually denoted by n!

                                                n!=1*2*3*…(n-2)*(n-1)*n

 It is also convenient do define 0!=1, so that the function is defined for all the non-negative integers.

Thus we have

         0!=1                         1!=1                        2!=2*1=2                              3!=3*2*1=6

4!=4*3*2*1=24                                              5!=5*4*3*2*1=120

And so on. Observe that

            5!=5*4! =5*24=120              and                6!=6*5!=6*120=720

That is true for every positive integer n; that is

                                                 n!=n*(n-1)!

 Definition: (Factorial Function)

      a)    If n=0, then n!=1

b)    If n>0, then n!=n*(n-1)!

Procedure: FACTORIAL (Fact, N)

This procedure calculates N! and return the value in the variable FACT.

 1.    If N=0, then: Set FACT:=1 and Return.

 2. Set FACT:=1 [Initialize FACT for loop.]

 3. Repeat for I =1 to N

Set FACT*=FACT*I

[End of loop]

4.   4. Return.

Procedure: FACTORIAL (Fact, N)

This procedure calculates N! and return the value in the variable FACT.

1.    If N=0, then: Set FACT:=1 and Return.

2.  Set FACT*=N*FACT

3.  Call FACTORIAL(FACT, N-1)

4.  Return.

Fibonacci sequence:

Fibonacci sequence usually denoted by(F0,F1,F2) as follows:

0,         1,         1,         2,         3,         5,         8,         13,       21,       34,       55..

That is, F=0 and F1=1 and each succeeding term is a sum of two preceding term:

For example, the next two term of a sequence is

34+55=89                              55+89=144

 

Def: (Fibonacci sequence)

a)    If N=0 or N=1, then Fn=n

b)    If n>1, then Fn=Fn-2+Fn-1

Procedure: FIBONACCI (FIB, N)

This procedure calculates Fn and return the value of in the first parameter FIB.

1. If  N=0 or N=1 , then: Set FIB:=N, and Return

2. Call FIBONACCI (FIBA, N-2)

3. Call FIBONACCI (FIBB, N-1)

4. Set FIB:=FIBA+FIBB.

5. Return.

Stacks & Stack Terminologies:

Stacks & Stack Terminologies:

A stack is a list of elements in which an element may be inserted or deleted only at one end, called the top of the stack.  This means, in particular, that the elements are removed from the stack in the reverse order of that in which they were inserted into a stack.

Special terminology used for two basic operations associated with stack:

1. Push:  is the term used to insert an element into a stack.
2. Pop:  is the term used to delete an element from a stack.
   

Array representation of Stacks:

Stack may be represented in the computer memory in various ways. Usually by means of one way list or a linear array. Stack will be maintained by linear array STACK. A pointer variable TOP, which contain the location of the top element of stack. And a variable MAXSTK which gives the maximum number of elements that can be held by the stack. The condition TOP= 0 or TOP=NULL will indicate the stack is empty.

Figure shows the array representation of stack. Since top = 3, the stack has three elements, XXX, YYY and ZZZ; and since MAXSTK=8, there is a room for five more elements in stack.

The operation of adding an element on to a stack and the operation of removing an element from the stack may be implemented, respectively, by the following procedure called push and pop.

In executing the procedure push, one must first check whether there is a room in the stack for the new item; if not, then we have the condition known as overflow.  Analogously, in executing the procedure pop, one must first test whether there is an element in the stack to be deleted; if not then we have the condition known as underflow.

Algorithm: PUSH (STACK, TOP, MAXSTK, ITEM)

This procedure Push an item onto a stack.

1.    [Stack already filled?]

If TOP= MAXSTK, then: print: OVERFLOW, and Return. 

2.    Set TOP:=TOP+1 [Increase TOP by 1]

3.    Set Stack [TOP]:=ITEM [Insert ITEM in new TOP position.]

4.    Return

Algorithm: POP (STACK, TOP, ITEM)

     This procedure Delete an item from a stack.

1.    [Stack has an item to be removed?]

If TOP= 0, then: print: UNDERFLOW, and Return. 

2.    Set ITEM :=STACK [TOP]  [Assign TOP element to ITEM.]

3.    Set Top: TOP-1. [Decrease TOP by 1.]

4.. Return

Polish notation:

In most common arithmetic operations, the operator symbol is placed between its two operand. 

For example, 

 A+B, C-D,    E*F,    G/H

This is called as infix notation.

Polish notation refers to the notation in which the operator symbol is placed before it's two operands also called as prefix notations.

For example, 

                                    +AB,   -CD,    *EF,    /GH

Translate following in this expression into polish (prefix) notation:

1. (A+B)*C=[+AB]*C=*+ABC
2. A+(B*C)=A+[*BC]= +A*BC
3. (A+B)/(C-D)=[+AB]/[-CD]=/+AB-CD

Reverse polish notation (postfix notation) refers to the analogous notation in which the operator symbol is place after two operand.

For example, 

                                    AB+,   CD+,   EF+,    GH+

Evaluation of Postfix Expression:

 

Suppose P is an arithmetic expression written in postfix notation.  The following algorithm, which uses a stack to hold the operands, evaluates P. 

Algorithm:  This algorithm finds the value of an arithmetic expression P written in postfix notation.

1. Add a right parentheses “)” at end of P. [This acts as a sentinel]
2. Scan P from left to right and repeat step 3 and 4 for each element of P until the sentinel is encountered.
3. If an operand is encountered, put it on STACK.
4. If an operator is encounter, then:

a)    Remove the top two element of stack, where A is the top element and B is the next top element.

b)    Evaluate  B X A

c)    Place the result of (b) back on STACK

        [End of if structure]

    5. Set VALUE equals to the top element on STACK

              6. Exit

Consider the following arithmetic expression P written in postfix notation:

                     P:        5,         6,         2,         +,         *,          12,       4,         /,          -

 Equivalent infix expression of Q follows:

                     Q: 5*(6+2)-12/4

 We evaluate P by simulating the above algorithm.  First we add a sentinel right parenthesis at the end of P to obtain

              P:        5,         6,         2,         +,         *,          12,       4,         /,          -

(1)       (2)       (3)       (4)       (5)           (6)       (7)       (8)       (9)

The elements of P have been labelled from left to right for easy reference.  Following figure shows the content of stack as each element of P is scanned, the final number in the stack is ,37,  which is assigned to the value when the sentinel “)” is scanned, is the value of P.

Two- Way List & Its Operations

Two Way Lists:

Two way lists is a linear collection of data elements, called nodes, where each node N is divided into three parts:

1. An information field INFO which contains data of node N.
2. A pointer field FORW which contains the location of the next node in the list.
3. A pointer Field BACK which contain the location of the preceding node in the list

The list also requires a pointer variable: FIRST, which points to the first node in the list, and LAST, which points to the last node in the list shown in figure.  Observe that NULL pointer appears in FORW field of the last node in the list and also in BACK field of the first node in the list:

Observe that using the variable FIRST and the pointer field FORW, we can traverse into a list in forward direction.  On the other hand using the variable LAST and pointer variable BACK we can also traverse the list in backward direction 

Suppose LOCA and LOCB are the locations, respectively, of node A and B in a two way list.  Then the way that the pointer FORW and BACK are define given us the following:

Pointer property: FORW [LOCA] = LOCB if and only if BACK [LOCB]:=LOCA

Deleting a node in Two-Way List:

Suppose we are given the location LOC of node N in LIST and suppose you want to delete N from the list. N is deleted from the list by changing the following pair of pointers.

FORW[BACK[LOC]]:= FORW[LOC] and BACK[FORW[LOC]]:=BACK[LOC]

  The deleted N is then returned to AVAIL list by the assignment:

                     FORW [LOC]:=AVAIL             and      AVAIL:=LOC

Algorithm: DELTWL (INFO, FORW, BACK, START, AVAIL, LOC)

1. [Delete node.]

            Set FORW [BACK [LOC]]:= FORW[LOC] and 

                BACK [FORW [LOC]]:=BACK[LOC]

         2.  [Return node to AVAIL list]

            Set FORW[LOC]:=AVAIL and AVAIL:=LOC

     3. Exit

Inserting a node in Two-Way List:

Suppose we are given the location LOCA and LOCB of adjacent nodes A and B in the list, and suppose we want to insert a given ITEM of information between nodes A node B.  As with a one way list, first we remove the first node N from the AVAIL list,  using the variable new to keep track of its location,  and then we copy the data ITEM into the node N,  we set:

 NEW: = AVAIL,         AVAIL: =FORW[AVAIL],      INFO[NEW]:=ITEM

 Now the node N with the content ITEM is inserted into the list by changing the following pair of pointers: 

                FORW[LOCA]:=NEW ,                   FORW[NEW]:=LOCB

                BACK[LOCB]:=NEW ,                  BACK[NEW]:=LOCA

Algorithm: INSTWL (INFO, FORW, BACK, START, AVAIL, LOCA, LOCB, ITEM)

1. [OVERFLOW?] If AVAIL=NULL, then: Write: OVERFLOW, and Exit

2.[Remove the node from list and copy new data into node

        Set NEW:= AVAIL,   AVAIL:=FORW[AVAIL],       INFO[NEW]

3.[Insert node into list]

        Set FORW[LOCA]:=NEW ,             FORW[NEW]:=LOCB

  BACK[LOCB]:=NEW ,              BACK[NEW]:=LOCA 

Header Linked List & Polynomials

Header Linked List:

Header linked list is a linked list which always contains a special node, all the header nodes at the beginning of the list.

The following are the two kinds of widely used header lists:

1. A grounded header list is a header list where the last node contains null pointer.
2. A circular header list is a header list where last node points back to the header node

Observe that the list pointer start always points to the header node, accordingly LINK[START]=NULL indicates that the grounded release is empty.  And LINK[START]=START  indicates the circular header list is empty.

 Algorithm: (Traversing a circular header list) Let List be circular header list  in memory. This algorithm traverses list, applying an operation process to each node of list.

1. Set PTR:=LINK[START] [Initialize the pointer PTR]
2.  Repeat steps 3 and 4 while PTR!= START
3.  Apply process to INFO[PTR] 
4. Set PTR:=LINK[PTR]  [PTR now point to next node]

        [ End of step 2 loop]

    5. Exit

Polynomials:

Header linked list are frequently used to maintain the polynomials in memory.  The header list plays an important part of this representation. 

Let p(x) denotes the following polynomial in one variable (containing four non zero terms):

                                             p(x)=2x8-5x7-3x2+4

 Then p(x) may be represented by the header linked list shown in figure, where each node corresponds to a non zero term p(x).  Specifically, the information part of the nod is divided into two field representing, respectively, the coefficient and the exponent of the corresponding term, and in node or link according to decreasing degree.

 Observe that the list pointer variable POLY points to the header node, whose exponent field is assign in negative number, in this case - 1.  Here the array representation of the linked list will require three linear arrays, which will call COEF, EXP and LINK.