Deletion a node from One-Way List.

Deletion from a Linked List:

Let list be a linked list with node N between node A and B, shown in figure.  Suppose node N is to be deleted from the linked list.  The schematic diagram of such deletion appears in figure.  The deletion occurs as soon as the next pointer field of node A is changed so that it points to node B( accordingly, when performing deletion, one must keep track of the address of the node which immediately precedes  the node that is to be deleted)

 Suppose our linked list is maintained in memory in the form of

                                    LIST( INFO, LINK, START, AVAIL) 

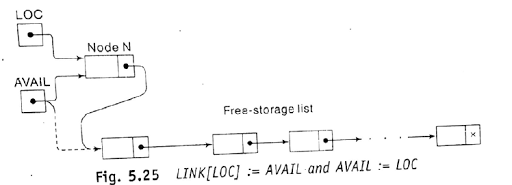
When node N is deleted from our list, we will immediately return its memory space to the AVAIL list. Specifically, for easier processing, it will be returned to the beginning of the AVAIL list.

1. The next pointer field of node A now points to node B, where node N previously pointed.
2. The next pointer field of N now points to the original of first node in the free pool, where the AVAIL previously pointed.
3.  The AVAIL now points to the deleted node N

Deletion algorithm:

Algorithms which delete nodes from linked list come up with various situations. The first one deletes the node following a given node, and the second one deletes the node with a given item of information.  Our entire algorithm assumes that the linked list is in memory in the form of LIST (INFO, LINK, START, AVAIL).

 All of our deletion algorithm will return the memory space of the deleted node and to the beginning of the AVAIL list. Accordingly,  all of our algorithm will include the following pair of assignment, where LOC is the location of the deleted node N

                                    LINK[LOC]:=AVAIL and AVAIL:=LOC

Deleting a node following a given node

Let LIST be a linked list in memory. Suppose we are given the location LOC of the node N in the list.  Furthermore, suppose we are given the location LOCP of the node preceding N or, when n is the first node, we are given LOCP=NULL 

Algorithm: DEL(INFO, LINK, START, AVAIL, LOC, LOCP)

This algorithm deletes the node N with the location LOC. LOCP is the location of the node which precedes N, or when N is the, LOCP=NULL.

1. If LOCP= NULL, then:

            Set START:=LINK[START]  [Delete first node]

        Else

            Set LINK[LOCP]:=LINK[LOC] [Delete node N]

    [End of If structure]

    2. [Return the deleted node to the AVAIL list]

            Set LINK[LOC]:= AVAIL and AVAIL:=LOC

               3.    Exit.