One- Way List & Its Operations

Linked List: 

Linked list or one way list is a linear collection of data elements, called nodes. Where linear order is given by means of pointers. Each node is divided into two parts:

·      The first part contains the information of the element.

·      The second part called the link field or the next pointer field contains the address of the next element in the list.

Figure shows a schematic diagram of linked list with 3 nodes

Each node is pictured with 2 parts. The left part contains the information of the node, which may contain an entire record of data items. The right part represents the next pointer field of the node.  The pointer of the last node contains a special value, called null pointer, which is having an invalid address.

In actual practice, 0 or a negative number used for the null pointer.  The null pointer signals the end of the list.  The linked list also contains a list pointer variable- START or Head- which contains the address of the first node in the list.  There is an arrow drawn from the start with the first node.

A special case is the list has no nodes, such list is called null list or empty list and is denoted by the null pointer in variable START or Head.

Representation of Linked List in memory:

Let list be a linked list.  The list will be maintained in memory, we require two linear arrays to store information and link the pointer field of the node in the list.  List also require a pointer variable start which contains the location of the beginning of the list and next pointer sentinel denoted by NULL-which indicates the end of the list

Traversing a Linked List:

Let List be a linked list in memory stored in a linear array INFO and LINK with start pointing to the first element and NULL indicates the end of the list. Suppose we want to traverse lists in order to process each node exactly once.

Traversing algorithm uses a pointer variable PTR which points to the node that is currently being processed. Accordingly, the LINK[PTR] points to the next node to be processed. Thus the assignment:

PTR: =LINK[ PTR]

Move the pointer to the next node in the list

Algorithm:  (Traversing) Let List be a linked list in memory. This algorithm traverses a list. Applying an operation to process each element of the list. Variable PTR point to the node current being processed

1. Set  PTR:=START [initializes pointer PTR]
2. Repeat steps 3 and 4 while PTR != NULL
3. Apply process to INFO[PTR]
4. Set PTR:=LINK[PTR] [ PTR now points to next node]

[End of Step 2 loop]

5.  Exit

Searching a Linked List:

List is Sorted: Suppose the data in the list are sorted. Then one searches for an item in the list by Traversing into a list using the pointer variable PTR and comparing the item with the content of INFO[PTR] of each node, one by one, of the list. 

                                    PTR:=LINK[PTR]

We require two tests. First we have to check to see whether we have reached the end of the list that is first we check to see whether:

                                    PTR =NULL

 If not, then we check to see whether:

INFO[PTR]=ITEM

Algorithm: Searching (INFO, LINK, START, ITEM, LOC)

List is a sorted list in memory. This algorithm finds the location LOC of the node where the item first appears in the list or sets LOC=NULL.

1.    Set  PTR:=START [initializes pointer PTR]

2.    Repeat steps 3 while PTR != NULL

3.    If ITEM < INFO[PTR], then:

        Set PTR:=LINK[PTR]   [PTR now points to next node]

    Else if ITEM=INFO[PTR], then:

        Set LOC:=PTR, and exit [Search is Successful]

    Else

        Set LOC:=NULL. And exit [ITEM now exceeds INFO[PTR]]

        [End of if Structure]

[End of Step 2 Loop]

4.    Set LOC:=NULL

5.    Exit

Memory Allocation:

The maintenance of the linked list in memory assumes the possibility of inserting new node into the list and hence required some mechanism which provides unused memory space for the new node

Some mechanism is required hereby the memory space of the deleted node becomes available for future use

Together with the linked list in memory, special this is maintained which consists of the unused memory cell,  which has its own pointer, is called the list of available space or storage list or free pool

Garbage Collection: 

The operating system of the computer periodically collects all the deleted space into a free storage list. Any technique which does this collection is called garbage collection.

Garbage Collection usually takes place in two steps. First the computer runs through all the list, tagging those cells which are currently in use, and then the computer runs through the memory and collects all the untagged space onto the free storage list. The garbage collection method takes place when there is only some minimum amount of space or no space left in a free storage list, or when the CPU is idle and has time to do the collection. Generally speaking garbage collection is invisible to the programmer.

Overflow and Underflow

Sometimes new data is to be inserted into a data structure but there is no available space that is a free storage list is empty. This situation is usually called Overflow.  The programmer may handle the overflow by printing the message overflow.  In such cases the programmer modified the program by adding space to the underlying array. Observe that overflow-will occur with our linked list when AVAIL=NULL and at the time of insertion. 

 The term Underflow refers to the situation where we want to delete the data from a data structure that is empty.  A programmer may handle underflow by printing message underflow.  Observe that underflow will occur with our linked list in START= NULL and at the time of deletion.

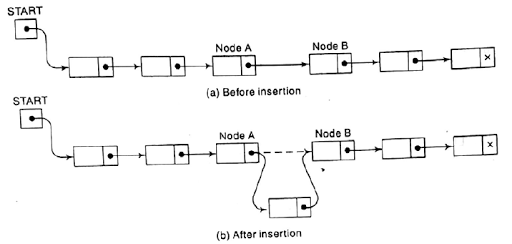
Insertion into a linked list:

Let the list be linked with successive nodes and A and B shown in figure. Suppose in node and is to be inserted into a linked list between node A and node B.

Suppose our linked list is maintained in memory in the form

                       LIST(INFO, LINK, START, AVAIL)

1. The next pointer field of node N now points to new node N, to which AVAIL previously pointed.
2. AVAIL now points to the second node in the free pool,, to which node N previously pointed
3.  The next pointer field of node N now points to node B, to which node A previously pointed.

Insertion algorithms:

1. Checking to see if the space is available in the AVAIL list.  if not, that is, if AVAIL=NULL then the algorithm will print the message  overflow.
2. Removing the first node from the AVAIL list. Using the variable NEW to keep track of the location of the new node, this type can be implemented by the pair of assignment

                         NEW:=AVAIL,    AVAIL:=LINK[AVAIL]

     3.    Copying new information into new node:

                                    INFO[NEW]:=ITEM

Inserting at the Beginning of the list:

Algorithm: INSBEG(INFO,LINK START, AVAIL, ITEM)

This algorithm inserts ITEM as the first node in the list.

1. [OVERFLOW?] If AVAIL=NULL, then: Write: OVERFLOW, and Exit.
2. [Remove first node from AVAIL list]

Set NEW:=AVAIL and AVAIL:=LINK[AVAIL]

3. Set INFO[NEW]:=ITEM [Copies new data into new node]
4. Set LINK[NEW]:=START [New node now points to original first]
5. Set START:=NEW. [Changes START so it points to the new node]
6. Exit.

Inserting after a given node:

Suppose we are given the value of LOC where LOC is a location of a node in a linked list or LOC = NULL.  This algorithm inserts ITEM into a list so that item follows node A or when LOC = NULL so that item is the first node.

Let N denote the new node.  if LOC=NULL, then N is inserted as the first node in the list.

Let node N point to node B:

                                    LINK[NEW]:=LINK[LOC]

And we let node A points to new node N by the assignment

LINK[LOC]:=NEW

Algorithm: INSLOC (INFO, LINK, START, AVAIL, LOC, ITEM)

1. [OVERFLOW?] If AVAIL=NULL, then: Write: OVERFLOW, and Exit.
2. [Remove first node from AVAIL list]

Set NEW:=AVAIL and AVAIL:=LINK[AVAIL]

3. Set INFO[NEW]:=ITEM [Copies new data into new node]
4. If LOC= NULL , then: [insert as a first node]

            Set LINK[NEW}:= START  and START:= NEW

            Else: [insert after node with location LOC]

                        Set LINK[NEW]:=LINK[LOC] and LINK[LOC]:= NEW

            [End of If structure]

5. Exit.

IDE of Visual Basic

Introduction:

Visual Basic Component Object Model (COM) Programming. It is first released in 1991.It is derived from BASIC and It is Rapid Application Development (RAD) of Graphical User Interface (GUI) applications

Visual programming tool refers to the environment which can be used to develop, debug and execute the graphical user interface (GUI) applications.

Rather than writing in numerous lines of code to describe the appearance and location or interface elements, the user simply drag and drop prebuilt objects placed on screen.

Visual programming tools integrate many different functions such as designs, editing, compiling   and debugging within a common environment therefore it is often referred to as Integrated Development Environment (IDE). 

The “Visual” part of Visual Programming refers to the method used to create the graphical user interface (GUI) applications which has a familiar appearance to the user.

The Microsoft Visual Basic development system is the most productive tool for creating high performance components and applications. Visual Basic is the Rapid application development(RAD) tool. Microsoft developed Visual Basic to make programming under Windows environment an easy process.

The BASIC parts refers to the BASIC( beginner's all-purpose invalid instruction code) language evolved  from the original basic language and now contains several hundred statements, functions and keywords, many of which relate directly to the windows GUI.

Features of Visual Basic:

•      Offers a set of predefined graphical objects

•      Response to mouse and keyboard actions(Events)

•      Provide set of predefined functions.

•      Provide set of predefined classes.

•      Full mathematical, string handling, and graphics functions

•      Handle fixed, dynamic and control arrays

•      Support modular programming(Procedures & Functions)

•      Sequential and random access file support

•      Debugger and error-handling facilities

•      Powerful database access tools

•      ActiveX support

Advantages of Visual Basic:

1. Users can develop the application in minimum time. 
2. The application developer is user friendly.
3. Applications are simple, yet powerful.
4. Maintenance (applying changes) of the application is easier.
5. Debugging an application are easier.

Structure of Visual Basic Application:

Application (Project) of VB contains:

• Forms - Windows that you create for user interface. 
• Controls - Graphical features drawn on forms to allow user interaction.
• Properties - Characteristic of a form or control is specified by a property.
• Methods - Built-in procedure that can be invoked some action to a particular object.
• Event Procedures -This is the code that is executed when a certain event occurs.
• General Procedures - This code must be invoked by the application.
• Modules -Collection of general procedures, variable declarations, and constant. 

How Event Driven Programming Works:

An event is an action recognized by a form or control. Event driven applications execute basic code in response to an event. Each form and control in Visual Basic has a predefined set of events. If one of these events of cause and there is a code in the associated events procedure, visual basic invoke that code

Although objects in Visual Basic automatically recognize a predefined set of events, it is up to you to decide if and how they will respond to a particular event.  A section of code- and event procedure- respond to each event. When you want  a control to respond to an event, you write code in the event procedure for that event.                              

The types of events recognized by an object vary, but many types are common to the most control.  For example, most objects recognized click events- If a user clicks a form, code in the form’s click event procedure is executed; if a user clicks a command button, code in the button’s click event procedure is executed.  The actual code in each case will most likely be quite different.

 Typical sequence of event in an event driven application:

1. The application starts and form is loaded and displayed.
2. The form (control on the form) receives an event. The event might be caused by the user ( a keystroke),  this system( A timer event),  or indirectly by your code.
3.  There is a code in the corresponding event procedure, it executes.
4.  The application waits for the next event

List of Events in VB:

Visual Basic startup dialog box:

Start>programs>Microsoft Visual Studio 6.0>Microsoft Visual Basic 6.0.

IDE of Visual Basic:

Menu Bar & Toolbar:

• Menu bar contains a standard command like: File, Edit, View,

    Window, Help menus, and specific command such as: Project, Format, or Debug menus.

• Toolbar contains the most commonly used commands (button), if clicked an action represented by that button is carried out.

Toolbox:

•It contains a collection of tools that are needed for project design.

•Tools are objects that could be selected from Toolbox to be placed on form.

•It  contains a set of controls that are used to place on a Form at design time thereby creating the user interface area.

Form Designer:

—It is a window for each form to customize the designed interface of the application.

—Using the form designer, the user can add controls, graphics, and text to create the desired form appearance.

Property Window:

—The Properties Window is used to set 

—It is used to display 

—The drop-down box at the top of the window lists all objects in the current form.

—Two views are available:

                               Alphabetic

                            Categorized

Project Explore Window:

Introduction to Data Structures

Data Structure can be defined as the group of data elements which provides an efficient way of storing and organizing data in the computer so that it can be used efficiently.

Some examples of Data Structures are arrays, Linked List, Stack, Queue, etc. Data Structures are widely used in almost every aspect of Computer Science i.e. operating System, Compiler Design, Artificial intelligence, Graphics and many more.

Data Structure is a way of data organization, management, and storage a data, which is used to access efficiently and also perform modifications. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data.

Data structures provide a means to manage large amounts of data efficiently for uses such as large databases

Data structures are generally based on the ability of a computer to fetch and store data at any place in its memory